Heap
모든 element에 대해서 heap-oreder 속성을 가지는 Complete Binary Tree이다.
- Heap은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 자료형이다.
- Heap에서 모든 노드에 대하여 자신의 자식보다 우선순위가 항상 높거나 낮아야 한다.
Min-Heap: 부모가 자식보다 우선순위가 항상 낮을 때Max-Heap: 부모가 자식보다 우선순위가 항상 높을 때
- 정렬을 할 때 직접 연결된 자식-부모간의 우선순위 비교만 하면 된다.
- 이진 트리는 각 노드마다 번호를 매길 수 있는데 가장 마지막 번호를 가지는 노드를
last node라 한다. - Height of Heap
- n개의 key가 저장된 힙은 O(logn)의 height를 가진다.
- 2^h - 1< n < 2^(h+1)-1를 통하여 도출 가능
Array Based Representation
Queue의 Array Based Representation 참고
Queue에서 다른점은 Heap은 완전 이진트리이다.
- Queue에서는 완전 이진트리가 아니므로 배열 사용에 공백이 있지만
- Heap은 완전 이진트리이므로 배열 사용에 공백이 없다.
- 따라서 Linked List보다 Array를 사용하는 것이 더 효율적이다.
Heap Insert / Deletion
Heapify: 우선순위에 따라 정렬되지 않은 것을 정렬하는 과정
Heap에서 필요한 요소들을 알아보자.
class Node{
int f = 0;
Node left(){
return A[f*2];
}
Node right(){
return A[f*2 + 1];
}
Node Parent(){
return A[f/2]; //c++에서는 나머지는 버림하므로 그대로 '/'연산을 한다.
// f/2의 값을 버림 연산을 한다.
}
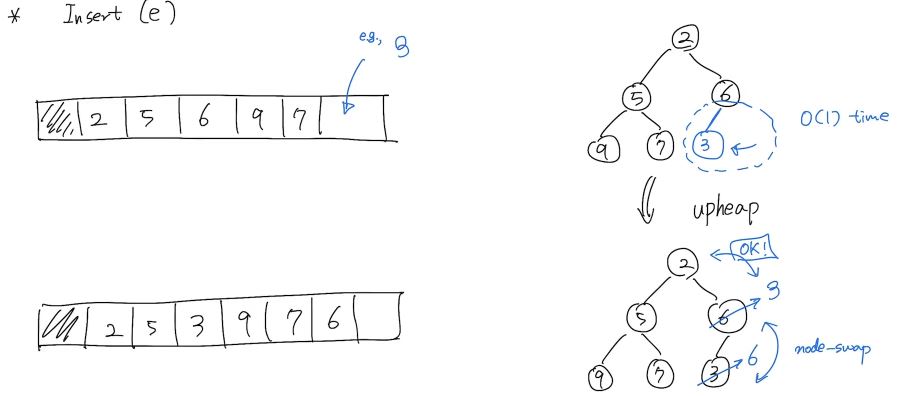
}insert(e): 요소 삽입
- 배열에서 마지막 저장소에 새 데이터를 저장한다.
- 자신의 부모와 우선순위를 비교한다.
- Unheap(우선순위대로 정렬되지 않았을 경우)할 경우
Heapify한다.
(부모와 자식의 위치를 Swap한다.)- 이를 Upheap이라 한다.
- Heap(우선순위대로 정렬되었을 경우)할 경우 함수를 종료한다.
- Unheap(우선순위대로 정렬되지 않았을 경우)할 경우
- Swap 후 다시 2번 과정을 Heap될 때 까지 반복한다.
- Upheap 알고리즘
Time Cost: O(logn)void Upheap(Node v){ while (v is not root && key(v) < key(parent(v))){ node_swap(v, parent(v)); v <- parent(v); } }
v가 최대 root까지 올라갈 수 있으므로 maximum h이다.
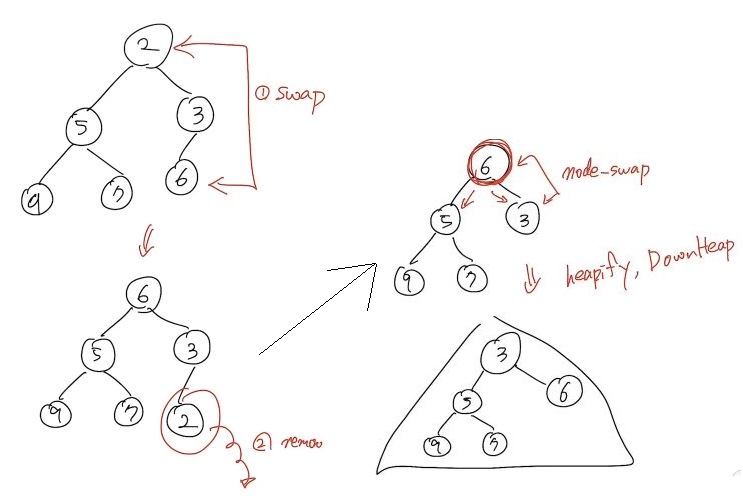
2^h <= n이므로 위 Cost가 나온다.removeMin(): 요소 삭제
- 삭제할 데이터(u)와 마지막 저장소에 저장된 데이터(v)를 Swap한다.
- 삭제할 데이터 u를 삭제한다.
- Swap된 v를 자식들과 우선순위를 비교한다.
- Unheap할 경우 Heapify한다.
부모와 자식의 위치를 바꾼다.- 이를 Downheap이라 한다.
- heap할 경우 함수를 종료한다.
- Unheap할 경우 Heapify한다.
- Swap한 후 다시 3번 과정을 Heap할 때 까지 반복한다.
- Downheap 알고리즘
Time Cost: O(logn)void Downheap(Node v){ while (v is not a leaf && key(v) < min(key(left(v),key(right(v))))){ u <- min(key(left(v),key(right(v)))); node_swap(v, u); v <- u; } }
v가 최대 leaf까지 내려갈 수 있으므로 maximum h이다.
2^h <= n이므로 위 Cost가 나온다.
In-place Heap Sort
Input된 데이터들을 그대로 받고 List로 내보낼 때 우선순위에 따라 내보낸다는 점에서
In-place Insertion Sort와 비슷하다. 참고
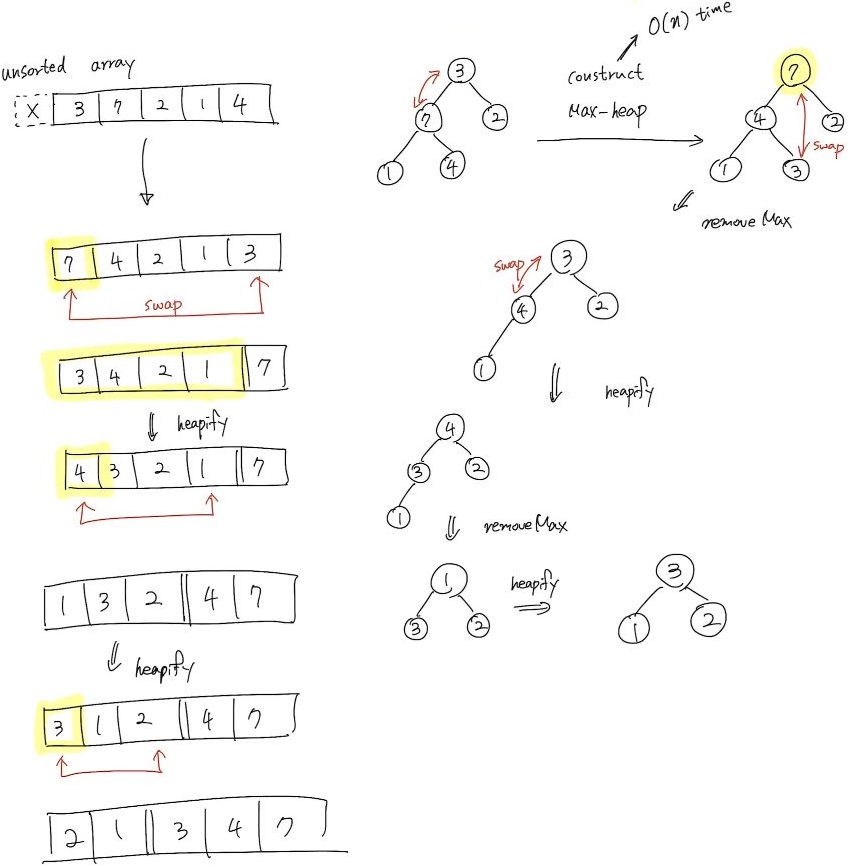
Max-heap으로 정렬된 상태에서 Heap Sort가 이루어진다.
- Input된 데이터 배열에 대해서 Max-heap으로 Construct한다.
- Unsorted 배열에서 우선순위가 가장 높은 데이터(=u)를 배열의 가장 마지막 저장소 Last Node(=v)와 Swap한다.
- u를 제거와 동시에 반환하고 현재 Heap에 Heapify를 수행한다.
- 2번과 3번 과정은 removeMax()를 수행하는 것과 같다.
- Heap에 남은 데이터가 없을 때 까지 2번부터 현재까지의 과정을 반복한다.
Time Cost: O(nlogn)
Heapify 할 때마다 log(n-i)가 소요가 된다. 이 과정이 총 n번 실시를 하므로 O(nlogn)이다.
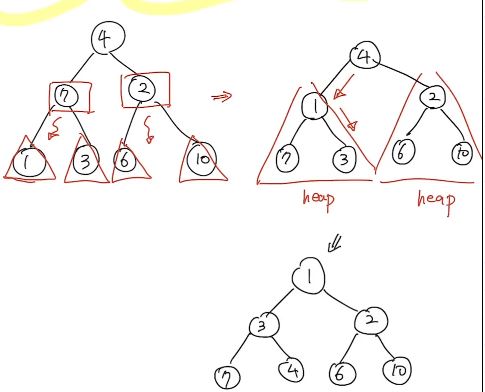
Bottom-up Heap construction
주어진 배열을 가장 낮은 Level부터 해서, 한 단계씩 Heapfy하면서 Heap을 만들어 나가는 구조
- 주어진 Tree를 최소한의
SubTree로 잘게 나누어 시작한다. - 그 SubTree를 Heapify를 하고 점차 더 큰 SubTree를 Heapfiy하여 root를 포함한 전체 Tree를 완성해 나가는 과정
- Time Cost: O(n)
- subtree의 수는 (2^(max h)-2)이다. 각 subtree에서 Heapify의 Complexity는 O(1)이므로 전체 Subtree에서 Heapify의 Time complexity는 (2^(max h)-2)O(1) => O(2^h)로 볼 수 있다.
- h는 최대 logn이므로 O(2^(logn)) = O(n)임을 알 수 있따.
'DataStructure' 카테고리의 다른 글
| Maps & Dictionary (0) | 2021.01.20 |
|---|---|
| Binary Search Tree (0) | 2021.01.20 |
| Tree (0) | 2021.01.19 |
| PriorityQueue(PQ) (0) | 2021.01.19 |
| Recursion (0) | 2021.01.19 |




최근댓글