PriorityQueue(PQ)
삽입되는 순서와 상관없이 우선순위에 따라 구조화되는 ADT
삽입 삭제는 key라고 불리는 우선순위로 결정된다.
key는 따로 정해진 것이 아닌 개발자가 정해주어야 한다.
Ex) 내림차순 정렬, 오름차순 정렬 etc..Queue는 Priority Queue의 일부이다.
Priority Queue Method
- insert
- 삽입 함수
- removeMin
- 우선순위가 가장 높은 항목을 제거한다.
- min
- 우선 순위가 가장 높은 항목을 보여준다.
- size
- 현재 저장된 요소의 수를 보여준다.
- empty
- 데이터가 저장되어있는지 확인한다.
Total Order Relations
모든 key에 대해 정의가 되어야 한다.
즉, 모든 key 값에 우선 순위가 매겨져야 한다.
Key
-
Key는 서로 다른 항목에서 같은 Key값을 가질 수 있다.
- key값이 x인 항목과 key값이 y인 항목이 있다면 x == y가 가능하다.
- 항상 x != y일 필요가 없다.
- key값이 x인 항목과 key값이 y인 항목이 있다면 x == y가 가능하다.
-
Key는 순서가 정의된 임의의 객체일 수 있다.
- Key가 꼭 숫자일 필요는 없다.
-
아래와 같이 객체를 통해 우선순위를 정해 줄 수 있다.
-
연산자 오버로딩으로 구현가능
Two ways to compare 2D points: class LeftRight { // left-right comparator public: bool operator()(const Point2D& p, const Point2D& q) const { return p.getX() < q.getX(); } }; class BottomTop { // bottom-top public: bool operator()(const Point2D& p, const Point2D& q) const { return p.getY() < q.getY(); } };
-
Priority Queue Sorting
이 메소드는 Priority Queue를 활용하여 우선순위에 맞게 리스트를 정렬해주고 반환하는 것이 목적이다.
먼저 PQ의 Sort 알고리즘을 확인하자
Algorithm PQ-Sort(S, C)
Input list S, 비교 연산자 C for the elements of S
Output C에 따라 오름차순으로 정렬된 리스트 S
P <- priority queue with comparator C;
while (!S.empty()) //1번 과정
e <- S.removeFront();
P.insert (e, C);
while (!P.empty()) //2번 과정
e <- P.removeMin();
S.addTail(e);1번 과정과 2번 과정의 차이에 따라
즉, P에 저장되는 방식에 따라
Priority Queue를 만드는데 Unsorted list와 Sorted list로 구분된다.Unsorted list: 1번 과정에서 리스트가 그대로 저장될 경우, 2번 과정에서 정렬됨. Selection Sort로 정렬된다.Sorted list: 1번 과정에서 정렬되고, 2번 과정에서 리스트가 그대로 전달될 경우, Selection Sort로 정렬된다.
Heap도 Priority Queue를 만들 수 있다.
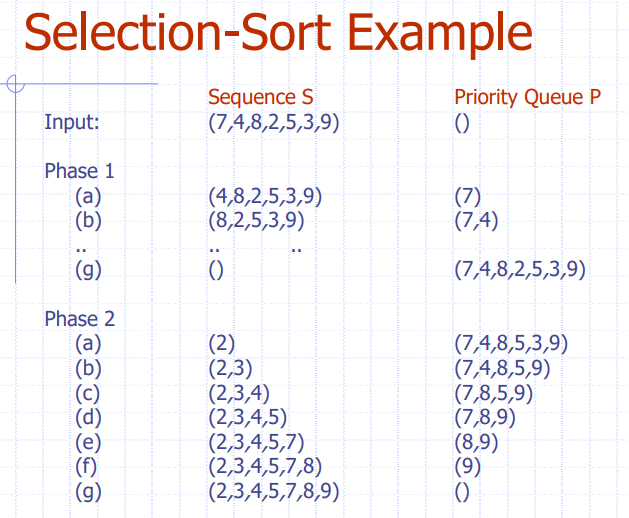
- Selection Sort: 2번 과정에서 List가 우선 순위에 따라 정렬 될 경우
- 1번 과정에서 P는 단순히 삽입 작업을 한다.
- 2번 과정에서 P는 리스트 S로 저장해주는데, 이때 P의 데이터에서 우선 순위에 따라 가장 높은 순으로 S로 전달한다. 즉, P의 데이터를 내보낼 때 우선 순위에 따라 내보내준다.
- Complexity 계산
- Time Cost: O(n^2)
- 1번 과정에서 단순히 삽입을 하므로 O(1) 이나, 2번 과정에서 총 n(n+1)/2의 time이 소요되었다. 따라서 O(n^2)이다.
- Space Cost: O(n)
- 기본적으로 입력되는 리스트가 n의 공간을 소요하나 추가적으로 소요되는 PQ는 리스트의 크기 n이므로 O(n)의 공간을 소요한다.
- 기본적으로 입력되는 리스트가 n의 공간을 소요하나 추가적으로 소요되는 PQ는 리스트의 크기 n이므로 O(n)의 공간을 소요한다.
- Time Cost: O(n^2)
- Insertion Sort: 1번 과정에서 List가 우선 순위에 따라 정렬 될 경우
- 1번 과정에서 S는 데이터를 저장된 순서대로 내보낸다. P에 저장될 때 우선 순위에 따라 저장된다.
- 2번 과정에서 P의 정보를 S로 단순 전달 작업을 한다.
- Complexity 계산
- Time Cost: O(n^2)
- 1번 과정에서 총 n(n+1)/2의 time이 소요되었다. 2번 과정에서는 단순히 전달 작업을 하므로 O(1) 이다. 따라서 O(n^2)이다.
- Space Cost: O(n)
- 기본적으로 입력되는 리스트가 n의 공간을 소요하나 추가적으로 소요되는 PQ는 리스트의 크기 n이므로 O(n)의 공간을 소요한다.
In-place Sort(제자리 정렬)정렬을 위해 기본 메모리를 제외한 추가적인 메모리를 사용하지 않음
In-place sort들은 오직 요소의 대체 또는 SWAP으로 정렬되어진다.
Ex) Bubble sort, heap sortm, 아래와 같은 insertion / selection sort가 해당함
- 기본적으로 입력되는 리스트가 n의 공간을 소요하나 추가적으로 소요되는 PQ는 리스트의 크기 n이므로 O(n)의 공간을 소요한다.
- Time Cost: O(n^2)
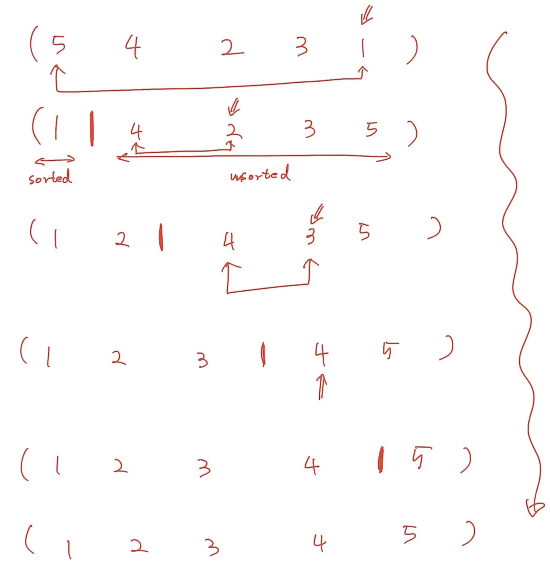
- In-place Insertion Sort
- i 번째의 루틴마다 우선순위가 높은 데이터를 i번의 비교를 통해 앞으로 보낸다.
- 이전 루틴에서 작업했던 요소들 다음 부터 처음까지 비교 연산을 하면서
(=i번째 작업에서i + 1요소부터 0번째 요소까지)
Swap을 통해 정렬해 나간다. - Bubble sort와 혼동되지 않기!
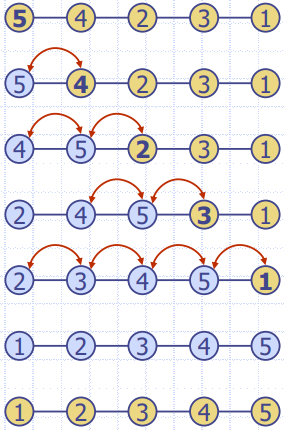
- In-place Selection Sort
- i 번째의 루틴에서 정렬되지 않은 데이터 리스트 중 우선순위가 가장 높은 데이터를 왼쪽으로 보낸다.
- i번째 작업에서 unsorted list에서 우선 순위가 가장 높은 데이터를 sorted list 바로 다음(i+1번째 요소)과 Swap한다.
- Bubble sort와 혼동되지 않기!
- 위 sort의 complexity
- Time Cost: O(n^2)
- 총 n번 루틴 동안 n(n+1)/2번의 swap이 있다. 따라서 O(n^2)이다.
- Space Cost: O(1)
- In-place이므로 O(1)이다.
- Time Cost: O(n^2)





최근댓글