Breadth-First Search
너비 우선 탐색: 신중하게 주변을 살피고 나아가는 traversal
자기 자신의 neighbors들을 모두 살피며 탐색함
알고리즘
BFS(G, v):
Q.enqueue(v);
mark v as "visited";
while(Q is not empty){
v <- Q.dequeue();
for w ∈ neighbors(v){
if w is "unvisited":
Q.enqueue(w);
mark w as "visited";
}
}Time Complexity
if G is represented as adjancency list: O(n+m)
알고리즘에 따른 경로
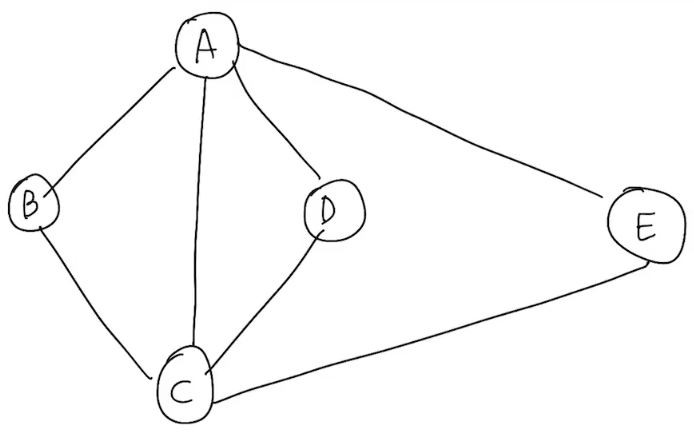
BFS(G, A):
mark A as "vistied"
- Q:[ A ]
- while state start, dequeue -> A
- Q: [ A ] -> [ ]
- B is A's neighbors and "Unvisited"
- Q: [ B ]
- mark B as "visited"
- C is A's neighbors, and "Unvisited"
- Q: [ B, C ]
- mark C as "visited"
- D is A's neighbors, and "Unvisited"
- Q: [ B, C, D ]
- mark D as "visited"
- E is A's neighbors, and "Unvisited"
- Q: [ B, C, D, E ]
- mark E as "visited"
- dequeue -> B
- Q: [ B, C, D, E ] -> [ C, D, E ]
- A is B's neighbors, but "visited"
- C is B's neighbors, but "visited"
- dequeue -> C
- Q: [ C, D, E ] -> [ D, E ]
- A is C's neighbors, but "visited"
- B is C's neighbors, but "visited"
- D is C's neighbors, but "visited"
- E is C's neighbors, but "visited"
- Q: [ C, D, E ] -> [ D, E ]
- dequeue -> D
- Q: [ D, E ] -> [ E ]
- A is D's neighbors, but "visited"
- C is D's neighbors, but "visited"
- dequeue -> E
- Q: [ E ] -> [ ]
- A is E's neighbors, but "visited"
- C is E's neighbors, but "visited"
=> A -> B -> C -> D -> E
용어
Hop
- 시작한 vertex를 기준으로 다른 vertex까지의 neighbor 관계
- 친구의 친구의 ...
- A에서 BCD는 1-hop 관계이다.
- A에서 EF는 2-hop 관계이다.
- i-hop 관계까지 edge의 수는 i개 이다.
- L_i에서 임의의 vertex v에 대해
- 시작 vertex부터 v까지 edge의 수는 i개이다.
- 그래프에서 s부터 v까지의 모든 경로는 최소 i개의 edge를 가진다.
- L_i에서 임의의 vertex v에 대해
- 시작한 vertex를 기준으로 다른 vertex까지의 neighbor 관계
Tree edge(= Discovery edge)
- Traversal 경로에 있는 edge
- 실선 화살표
Cross edge
탐색을 하려 했으나 이미 "Visted"된 vertex라 가지 못한 edge
점선 화살표
cross edge가 아닌 두 개의 vertices의 level 수 차이는 최대 1이다.
- pf) BFS는 현재의 vertex에서 연결된 edge들을 먼저 모두 방문을 하기 때문에 만일 level 2 이상 차이나는 edge가 존재한다면, 그 이미 해당 vertex에서 첫번째로 방문한 것이다.
따라서, 이미 2이상 차이나는 edge는 cross edge일 것이다.
- pf) BFS는 현재의 vertex에서 연결된 edge들을 먼저 모두 방문을 하기 때문에 만일 level 2 이상 차이나는 edge가 존재한다면, 그 이미 해당 vertex에서 첫번째로 방문한 것이다.
Back edge와 다르다
BFS Tree
- tree edge로 연결된 subgraph
- BFS Spanning Tree
- 모든 vertex를 가지므로 Spanning tree이다.
DFS vs BFS
'DataStructure' 카테고리의 다른 글
| Depth-First Search(DFS) (0) | 2021.01.20 |
|---|---|
| Graph (0) | 2021.01.20 |
| Hash Tables (0) | 2021.01.20 |
| AVL Tree (0) | 2021.01.20 |
| Maps & Dictionary (0) | 2021.01.20 |




최근댓글