Depth-First Search
깊이 우선 탐색: 일단 나아가고 보는 traversal
ex) Preorder, Post order traversal
Algorithm
DFS(G, v):
mark v as "vistied";
for each ∈ neighbors(v):
if w is "unvisited":
DFS(G, u);Time Complexity
if G is represented as adjancency list: O(n+m)
In matrix: O(n^2)
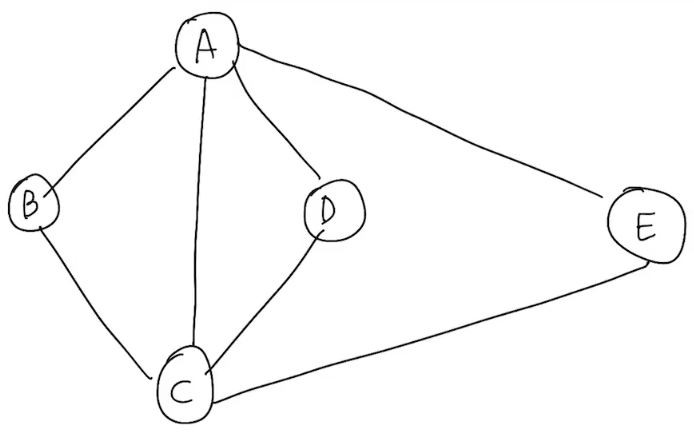
알고리즘에 따른 경로
DFS(G, A):
mark A as "visited"
- B is A's neighbors
- DFS(G, B)
mark B as "visited"
- C is B's neighbors
- DFS(G, C)
mark C as "visited"
- A is C's neighbors
- but, A is "visited"
- D is C's neighbors
- DFS(G, D)
- mark D as "visited"
- A is D's neighbors
- but, A is "visited"
- there is no neighbors
- return back
- A is D's neighbors
- In C's DFS(G, C), find C's neighbors
- E is C's neighbors
- DFS(G, E)
- mark E as "visited"
- all neighbors is "visited"
- return
- all neighbors is "visited"
- return
- A is C's neighbors
- all neighbors is "visited"
- return
- all neighbors is "visited"
- return
=> A -> B -> C -> D -> E의 순서로 traversal 한다.
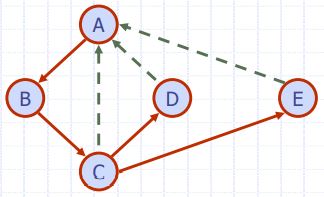
용어
- Tree edge(= Discovery edge)
- Traversal 경로에 있는 edge
- 붉은 화살표
- Back edge
- 탐색을 하려 했으나 이미 "Visted"된 vertex라 가지 못한 edge
- 점선 화살표
- 이 edge가 존재하면, cycle이 존재함을 알려준다.
- Cross edge와 다르다
- DFS Tree
- tree edge로 연결된 subgraph
- DFS Spanning Tree
- 모든 vertex를 가지므로 Spanning tree이다.
- DFS Tree를 다시 그려보면 다음과 같다.
Finding method
Path Finding: vertex에서 다른 vertex로 가는 경로를 알려준다.
Algorithm
Algorithm pathDFS(G, v, z) Input graph G =(V, E) and a start vertex v ∈ V S.push(v) mark v as VISITED if v = z return S.elements() for all w ∈ {neighbors of v} if w is marked as UNVISITED pathDFS(G, w, z) S.pop(v)- O(n+m) Time
Cycle Finding: cycle path를 알려준다.
Algorithm
Algorithm cycleDFS(G, v) S.push(v); //여기서부터 mark v as VISITED; for all w ∈ {neighbors of v} if (w, v) is UNEXPLORED; if w is marked as UNVISITED mark (w, v) as EXPLORED; cycleDFS(G, w); //여기까지 basic DFS와 같다. else // back edge를 찾았을 때 T <- new empty stack; while(o != w); o <- S.pop(); T.push(o); return T.elements(); S.pop(v);- O(n+m) Time
DFS vs BFS
'DataStructure' 카테고리의 다른 글
| Breadth-First Search(BFS) (0) | 2021.01.20 |
|---|---|
| Graph (0) | 2021.01.20 |
| Hash Tables (0) | 2021.01.20 |
| AVL Tree (0) | 2021.01.20 |
| Maps & Dictionary (0) | 2021.01.20 |





최근댓글